
题目列表(包括答案和解析)
(本小题满分6分)
在如图所示的直角坐标系中,O为原点,直线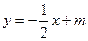 与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且
与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且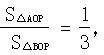 ,试求点P的坐标.
,试求点P的坐标.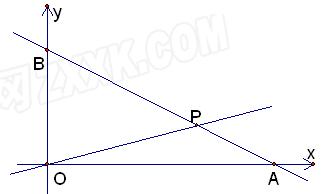
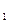 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q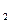 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用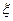 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为 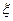 | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3 | P4 |
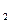 的值;
的值; 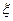 的数学期望E
的数学期望E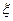 ;
;(本小题满分12分)
在平面直角坐标系xOy中,抛物线的解析式是y =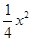 +1,点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
+1,点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
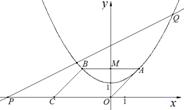
(1) 写出点M的坐标;
(2) 当四边形CMQP是以MQ,PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围;
② 当梯形CMQP的两底的长度之比为1:2时,求t的值.
(本小题满分10分)
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点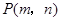 的横坐标,第二个数作为点
的横坐标,第二个数作为点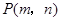 的纵坐标,则点
的纵坐标,则点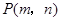 在反比例函数
在反比例函数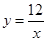 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数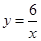 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点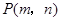 的情形;
的情形;
(2)分别求出点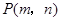 在两个反比例函数的图象上的概率,并说明谁的观点正确。
在两个反比例函数的图象上的概率,并说明谁的观点正确。
(本小题满分10分)在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为![]() (0°<
(0°<![]() <180°),得到△A1B1C.
<180°),得到△A1B1C.

(1)如图1,当AB∥CB1时,设A1B1与BC相交于点D.证明:△A1CD是等边三角形;
(2)如图2,连接AA1、BB1,设△ACA1和△BCB1的面积分别为S1、S2.
求证:S1∶S2=1∶3;
(3)如图3,设AC的中点为E,A1B1的中点为P,AC=a,连接EP.当![]() 等于多少度时,EP的长度最大,最大值是多少?
等于多少度时,EP的长度最大,最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com