
题目列表(包括答案和解析)
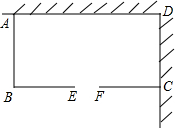 (2011•香坊区模拟)如图,用长为18米的篱笆两面靠墙围成一个矩形苗圃ABCD,其中EF是一个2米宽的门(门不需要篱笆).设边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).
(2011•香坊区模拟)如图,用长为18米的篱笆两面靠墙围成一个矩形苗圃ABCD,其中EF是一个2米宽的门(门不需要篱笆).设边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米). 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗
 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com