练习册

  • 练习册
  • 试题
    [05温州]如图.在Rt△ABC中.已知AB＝BC＝CA＝4cm.AD⊥BC于D.点P.Q分 别从B.C两点同时出发.其中点P沿BC向终点C运动.速度为1cm/s,点P沿CA.AB向终点B运动.速度为2cm/s.设它们运动的时间为x(s). ⑴ 求x为何值时.PQ⊥AC, ⑵ 设△PQD的面积为y(cm2).当0＜x＜2时.求y与x的函数关系式, ⑶ 当0＜x＜2时.求证:AD平分△PQD的面积, ⑷ 探索以PQ为直径的圆与AC的位置关系.请写出相应位置关系的x的取值范围 [解] ⑴ ∵当Q在AB上时.显然PQ不垂直于AC. 当.由题意得:BP＝x.CQ＝2x.PC＝4-x. ∴AB＝BC＝CA＝4.∠C＝600. 若PQ⊥AC.则有∠QPC＝300.∴PC＝2CQ ∴4-x＝2×2x.∴x＝. ∴当x＝时.PQ⊥AC, ⑵ 当0＜x＜2时.P在BD上.Q在AC上.过点Q作QH⊥BC于H. ∵∠C＝600.QC＝2x.∴QH＝QC×sin600＝x ∵AB＝AC.AD⊥BC.∴BD＝CD＝BC＝2 ∴DP＝2-x.∴y＝PD·QH＝(2-x)·x＝- ⑶ 当0＜x＜2时.在Rt△QHC中.QC＝2x.∠C＝600. ∴HC＝x.∴BP＝HC ∵BD＝CD.∴DP＝DH. ∵AD⊥BC.QH⊥BC.∴AD∥QH. ∴OP＝OQ ∴S△PDO＝S△DQO. ∴AD平分△PQD的面积, ⑷ 显然.不存在x的值.使得以PQ为直径的圆与AC相离 当x＝或时.以PQ为直径的圆与AC相切. 当0≤x＜或＜x＜或＜x≤4时.以PQ为直径的圆与AC相交. 【查看更多】

     

    题目列表(包括答案和解析)

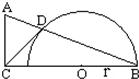    19、如图，在Rt△ABC中，已知∠ACB=90°，O为BC边上一点，以O为圆心，OB为半径作半圆与AB边交于点D，连接CD，若CD恰好是⊙O的切线：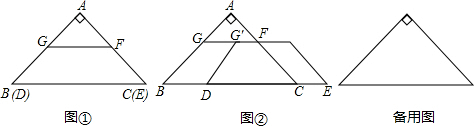
    （1）求证；△CAD是等腰三角形；
    （2）若AC=3，BC=5，求⊙O的半径r．

    查看答案和解析>>

    如图①，在Rt△ABC中，已知∠A=90°，AB=AC，G、F分别是AB、AC上的两点，且GF∥BC，AF=2，BG=4．
    （1）求梯形BCFG的面积；
    （2）有一梯形DEFG与梯形BCFG重合，固定△ABC，将梯形DEFG向右运动，直到点D与点C重合为止，如图②．
    ①若某时段运动后形成的四边形BDG'G中，DG⊥BG'，求运动路程BD的长，并求此时G'B2的值；
    ②设运动中BD的长度为x，试用含x的代数式表示出梯形DEFG与Rt△ABC重合部分的面积S．精英家教网

    查看答案和解析>>

    利用图形，我们可以求出tan30°的值．如图，在Rt△ABC中，已知∠C=90°，AB=2，AC=1，可求出∠B=30°，tan30°=
    AC
    BC
    =
    1
    		3
    =
    		3
    3
    ．在此图的基础上，我们还可以添加适当的辅助线，求出tan15°的值，请你动手试一试．

    查看答案和解析>>

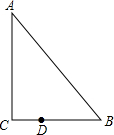    （2012•夹江县模拟）如图，在Rt△ABC中，已知∠C=90°，∠B=50°，点D在边BC上，BD=2CD．现将△ABC绕着点D按逆时针旋转一定的角度后，使得点B恰好落在初始Rt△ABC的边上．设旋转角为α（0°＜α＜180°），那么α=
    80°或120°
    80°或120°
    ．

    查看答案和解析>>

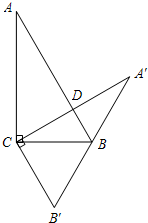    （2006•上海模拟）如图，在Rt△ABC中，已知∠ACB=90°，∠A=30°，BC=4．以点C为旋转中心把△ABC旋转到△A′B′C，点B在边A′B′上，边A′C与边AB相交于点D．求△ABC与△A′B′C重叠部分的面积．

    查看答案和解析>>


    同步练习册答案