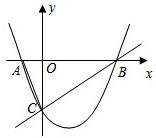如图1，已知：抛物线与x轴交于A、B两点，与y轴交于点C，经过B、C两点的直线是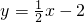，连接AC．
（1）写出B、C两点坐标，并求抛物线的解析式；
（2）判断△ABC的形状，并说明理由；
（3）若△ABC内部能否截出面积最大的矩形DEFG（顶点D、E、F、G在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．
{抛物线y=ax²+bx+c的顶点坐标是}．

已知等边三角形纸片ABC的边长为8，D为AB边上的点，过点D作DG∥BC交AC于点G．DE⊥BC于点E，过点G作GF⊥BC于点F，把三角形纸片ABC分别沿DG，DE，GF按图1所示方式折叠，点A，B，C分别落在点，，处．若点，，在矩形DEFG内或其边上，且互不重合，此时我们称△(即图中阴影部分)为“重叠三角形”．

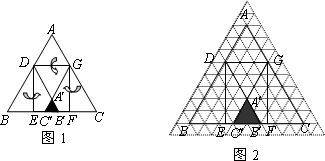
(1)若把三角形纸片ABC放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形)，点A，B，C，D恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠三角形的面积；

(2)实验探究：设AD的长为m，若重叠三角形存在．试用含m的代数式表示重叠三角形的面积，并写出m的取值范围(直接写出结果，备用图供实验，探究使用)．

解：(1)重叠三角形的面积为________；

(2)用含m的代数式表示重叠三角形的面积为________；m的取值范围为________．