
题目列表(包括答案和解析)
| a |
| a |
| a2 |
| a |
| b |
| ab |
| ||
|
|
| c |
| c |
| c |
| n | a |
| 3 | -16 |
| 3 | 2 |
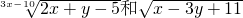 是同类二次根式.
是同类二次根式.下列说法中:
①4的算术平方根是±2;②![]() 与
与![]() 是同类二次根式;③点
是同类二次根式;③点![]() 关于原点对称的点的坐标是
关于原点对称的点的坐标是![]() ;④抛物线
;④抛物线![]() 的顶点坐标是
的顶点坐标是![]() 其中正确的是( )
其中正确的是( )
A.①②④ B.①③ C.②④ D.②③④
下列说法中:
①4的算术平方根是±2;
②![]() 与
与![]() 是同类二次根式;
是同类二次根式;
③点![]() 关于原点对称的点的坐标是
关于原点对称的点的坐标是![]() ;
;
④抛物线![]() 的顶点坐标是
的顶点坐标是![]()
其中正确的是( )
A.①②④ B.①③ C.②④ D.②③④
下列说法中:
①4的算术平方根是±2;
②![]() 与
与![]() 是同类二次根式;
是同类二次根式;
③点![]() 关于原点对称的点的坐标是
关于原点对称的点的坐标是![]() ;
;
④抛物线![]() 的顶点坐标是
的顶点坐标是![]()
其中正确的是( )
A.①②④ B.①③ C.②④ D.②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com