23、响水中学七年级9班学生小若,在学习了统计图的制作和变量的关系的知识后,想给自己制作一张反映自己学习成绩成长趋势的统计图,以了解自己学习成绩的变化趋势.
于是,他请教了数学老师,数学老师给了他两个建议:
(1)制作什么统计图才能反映成绩的变化趋势;
(2)试卷有难有易,试题难时,分数低不一定表示退步,如何才能客观地、较正确地反映自己的成绩的变化趋势?
小若回家后经过仔细思索,认为应制作
折线
统计图才能反映成绩的变化趋势;其次,应把自己每次考试成绩与班级平均分比较,即:每次考试成绩X减去班级平均分Y,为避免出现负分,再加上60分,称为成长分值A,用公式表示为:A=X-Y+60这个关系式里有几个变量,因变量是
成长分值A
.
小若兴冲冲地把自己的想法告诉了数学老师,数学老师高度表扬了小若,认为小若是个爱动脑筋且能活学活用、有创新意识的孩子,如果能够持之以恒,前途不可限量.小若很快从老师那儿拿到了自己的各次考试成绩,以及相应的班级各次平均分,请你帮小若算出他的各次成长分值,以及帮小若画出他的成长趋势图.

(3)填出上表的各章考试的成长分值,并画出小若的成长趋势图:

(4)按照小若的成长趋势,请你预测小若第五章的成长分值A是
90
分.理由是:

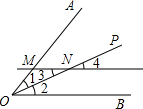
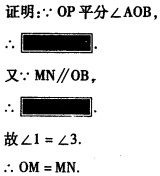
 请你在括号内填上下面解答过程中不完整的内容和理由.
请你在括号内填上下面解答过程中不完整的内容和理由. 请你在括号内填上下面解答过程中不完整的内容和理由.
请你在括号内填上下面解答过程中不完整的内容和理由.