
题目列表(包括答案和解析)
(2011山东烟台,26,14分)
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=-![]() x+
x+![]() ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
(3)当t为何值时s有最大值?并求出最大值.
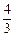 x+
x+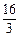 ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(2011山东烟台,26,14分)
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=-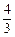 x+
x+ ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
(3)当t为何值时s有最大值?并求出最大值.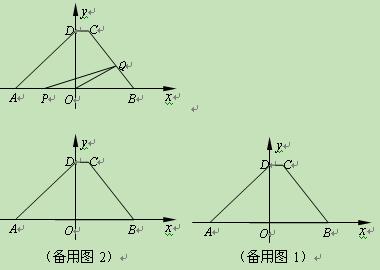
(2011山东烟台,26,14分)
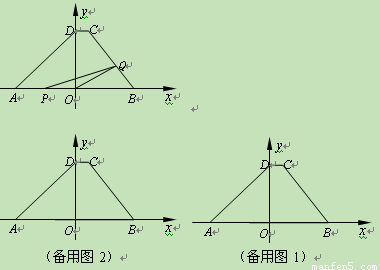
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=-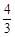 x+
x+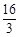 ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
(3)当t为何值时s有最大值?并求出最大值.
| 1 |
| 2 |
| 5 |
| 9 |
| 5 |
| 6 |
| 7 |
| 12 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 15 |
| 8 |
| 10 |
| 3 |
| 15 |
| 4 |
| 17 |
| 18 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com