
题目列表(包括答案和解析)
(湖北卷)(本小题满分14分)
已知不等式![]() 为大于2的整数,
为大于2的整数,![]() 表示不超过
表示不超过![]() 的最大整数. 设数列
的最大整数. 设数列![]() 的各项为正,且满足
的各项为正,且满足![]()
(Ⅰ)证明![]()
(Ⅱ)猜测数列![]() 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当![]() 时,对任意b>0,都有
时,对任意b>0,都有![]()
(本小题 10 分)如图,在 Rt△ABC中,∠ACB=90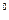 D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
( 1 )求证: BD =" BF" ;
( 2 )若 BC =" 12" , AD =" 8" ,求 BF 的长.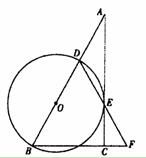
(本小题10分)
如图,在平面直角坐标系中, 的三个顶点的坐标分别为
的三个顶点的坐标分别为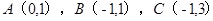 .
.
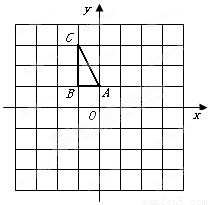
1.(1)画出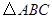 关于x轴对称的
关于x轴对称的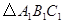 ,并写出点
,并写出点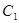 的坐标.
的坐标.
2.(2)画出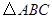 绕原点
绕原点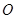 顺时针方向旋转90°后得到的
顺时针方向旋转90°后得到的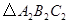 ,并写出点
,并写出点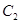 的坐标.
的坐标.
3.(3)将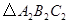 平移得到
平移得到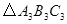 ,使点
,使点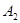 的对应点是
的对应点是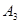 ,点
,点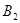 的对应点是
的对应点是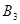 ,点
,点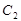 的对应点是
的对应点是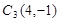 ,在坐标系中画出
,在坐标系中画出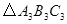 ,并写出点
,并写出点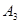 ,
,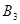 的坐标.
的坐标.
(本小题10分)如图,已知圆锥的底面半径为10 ,母线长为40 .
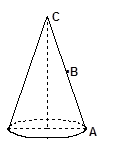
(1)求圆锥侧面展开图的圆心角;
(2)若一小虫从点A出发沿圆锥侧面绕行到母线CA的中点B处,求它所走的最短路程是多少?
(11·湖州)(本小题10分)
我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表:
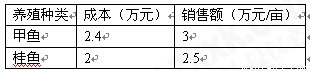
⑴2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共收益多少万元?(收益=销售额-成本)
⑵2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
⑶已知甲鱼每亩需要饲料500㎏,桂鱼每亩需要饲料700㎏,根据⑵中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少㎏?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com