
题目列表(包括答案和解析)
(本小题满分10分)
在图1至图3中,直线MN与线段AB相交
于点O,∠1 = ∠2 = 45°.

1.(1)如图1,若AO = OB,请写出AO与BD
的数量关系和位置关系;
2.(2)将图1中的MN绕点O顺时针旋转得到
图2,其中AO = OB.
求证:AC = BD,AC ⊥ BD;
3.(3)将图2中的OB拉长为AO的k倍得到
图3,求![]() 的值.
的值.
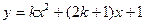 (
(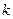 为实数)
为实数)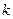 ,函数的图像都具有的特征,并给予证明;
,函数的图像都具有的特征,并给予证明;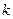 ,当
,当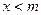 时,
时,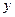 随着
随着 的增大而增大,试求出
的增大而增大,试求出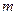 的一个值
的一个值(本小题满分10分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
 ,cos41°=
,cos41°= ,tan37°=
,tan37°= )
)



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com