七年级学生小明剪出了多张如图⑴中的正方形和长方形的卡片，利用这些卡片他拼成了如图⑵中的大正方形，由此验证了我们学过的公式：．现在请你选取图⑴中的卡片（各种卡片的张数不限），并利用它们在图⑶中拼出一个长方形，由此来验证等式：．（请按照图⑴中卡片的形状来画图，并像图⑵那样标上每张卡片的代号）．

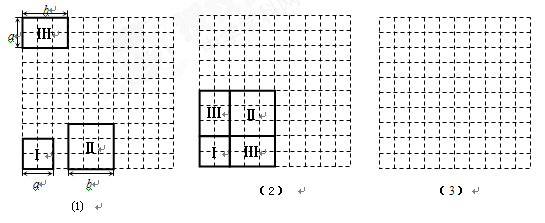
【解析】本题考查的是对完全平方公式的理解应用程度，用几何图形推导代数恒等式时要注意整体图形面积与部分图形面积之间的关系

有两个可以自由转动的均匀的转盘A 、B，转盘分别分为4与3等分，及标有数字，（如图）。小明与小聪同学用这两个转盘做游戏，游戏规则如下：① 分别转动转盘A与B一次：

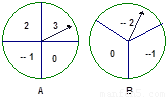
② 转盘停止后，将指针所指的数字相加（如果指针恰好停在等分线上，则重转，直到指针指向某一数字为止）如果和为非负数，小明胜，否则小聪胜。 

⑵   用列表或树状图求小明获胜的概率。

        ⑵ 你认为游戏公平吗？请说明理由。

【解析】本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平, 概率=所求情况数与总情况数之比

有两个可以自由转动的均匀的转盘A 、B，转盘分别分为4与3等分，及标有数字，（如图）。小明与小聪同学用这两个转盘做游戏，游戏规则如下：①分别转动转盘A与B一次：

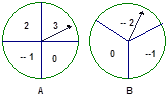
② 转盘停止后，将指针所指的数字相加（如果指针恰好停在等分线上，则重转，直到指针指向某一数字为止）如果和为非负数，小明胜，否则小聪胜。 

⑵   用列表或树状图求小明获胜的概率。

        ⑵ 你认为游戏公平吗？请说明理由。

【解析】本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平, 概率=所求情况数与总情况数之比

解不等式组：并把解集在数轴上表示出来.

【解析】本题考查的是解不等式组及在数轴上表示不等式解集的方法

七年级学生小明剪出了多张如图⑴中的正方形和长方形的卡片，利用这些卡片他拼成了如图⑵中的大正方形，由此验证了我们学过的公式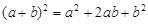：．现在请你选取图⑴中的卡片（各种卡片的张数不限），并利用它们在图⑶中拼出一个长方形，由此来验证等式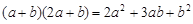：．（请按照图⑴中卡片的形状来画图，并像图⑵那样标上每张卡片的代号）．

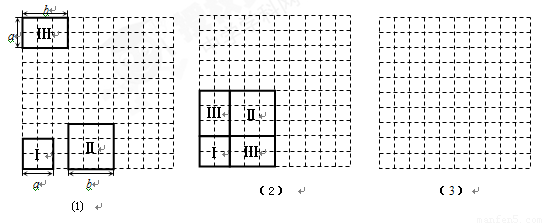
【解析】本题考查的是对完全平方公式的理解应用程度，用几何图形推导代数恒等式时要注意整体图形面积与部分图形面积之间的关系