
题目列表(包括答案和解析)
如图,四面体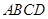 中,
中,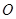 、
、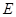 分别是
分别是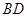 、
、 的中点,
的中点,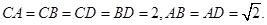
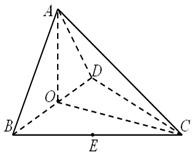
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角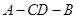 的正切值;
的正切值;
(Ⅲ)求点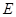 到平面
到平面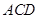 的距离.
的距离.
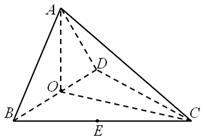
如图,四面体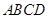 中,
中,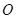 、
、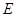 分别是
分别是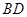 、
、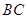 的中点,
的中点,
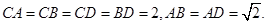
(Ⅰ)求证: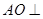 平面
平面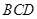 ;
;
(Ⅱ)求异面直线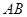 与
与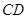 所成角余弦值的大小;
所成角余弦值的大小;
(Ⅲ)求点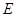 到平面
到平面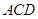 的距离.
的距离.
如图,四面体 中,
中, 、
、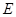 分别是
分别是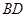 、
、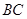 的中点,
的中点,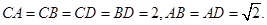
(1)求证: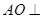 平面
平面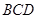 ;
;
(2)求直线 与平面
与平面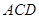 所成角的余弦值;
所成角的余弦值;
(3)求点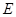 到平面
到平面 的距离。
的距离。
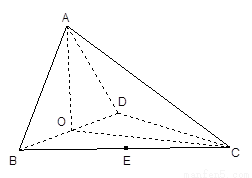
如图,四面体 中,
中, 、
、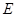 分别是
分别是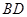 、
、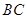 的中点,
的中点,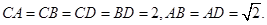
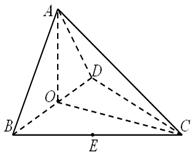
(Ⅰ)求证: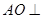 平面
平面 ;
;
(Ⅱ)求二面角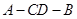 的正切值;
的正切值;
(Ⅲ)求点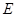 到平面
到平面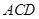 的距离.
的距离.
如图,四面体 中,
中, 、
、 分别是
分别是 、
、 的中点,
的中点,
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求异面直线 与
与 所成角余弦值的大小;
所成角余弦值的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
一、填空题:
1.试题.files/image250.gif) 2.
2.试题.files/image252.gif) 3.
3.试题.files/image254.gif) 4.
4.试题.files/image256.gif) 5.
5.试题.files/image258.gif) 6.
6.试题.files/image260.gif) 7.
7.试题.files/image262.gif) 8.2009 9.4个 10.①② 11.
8.2009 9.4个 10.①② 11.试题.files/image264.gif)
二、选择题:
12.B 13.C 14.D 15.D
三、解答题:
16.解:(Ⅰ)因为试题.files/image145.gif) 点的坐标为
点的坐标为试题.files/image154.gif) ,根据三角函数定义可知
,根据三角函数定义可知试题.files/image267.gif) ,
,
试题.files/image269.gif) ,
,试题.files/image271.gif) , 2分
, 2分
所以试题.files/image273.gif) 4分
4分
(Ⅱ)因为三角形试题.files/image156.gif) 为正三角形,所以
为正三角形,所以试题.files/image275.gif) ,
,试题.files/image277.gif) ,
,试题.files/image279.gif) ,
5分
,
5分
所以试题.files/image281.gif)
试题.files/image283.gif) 7分
7分
所以试题.files/image285.gif)
试题.files/image287.gif) 。
11分
。
11分
17.方法一:(I)证明:连结OC,因为试题.files/image289.gif) 所以
所以试题.files/image291.gif)
又试题.files/image293.gif) 所以
所以试题.files/image295.gif) ,
2分
,
2分
在试题.files/image297.gif) 中,由已知可得
中,由已知可得试题.files/image299.gif) 而
而试题.files/image301.gif)
所以试题.files/image303.gif) 所以
所以试题.files/image305.gif) 即
即试题.files/image307.gif) ,
,
而试题.files/image309.gif) 所以
所以试题.files/image175.gif) 平面
平面试题.files/image312.gif) 。
5分
。
5分
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知试题.files/image314.gif)
所以直线OE与EM所成的锐角就是异面直线AB与CD所成的角, 7分
在试题.files/image316.gif) 中,
中,试题.files/image318.gif) 因为
因为试题.files/image320.gif) 是直角
是直角试题.files/image297.gif) 斜边AC上的中线,所以
斜边AC上的中线,所以试题.files/image323.gif) 所以
所以试题.files/image325.gif)
所以异面直线AB与CD所成角的大小为试题.files/image327.gif) 。
12分
。
12分
18.解:(Ⅰ)由年销售量为试题.files/image187.gif) 件,按利润的计算公式,有生产A、B两产品的年利润
件,按利润的计算公式,有生产A、B两产品的年利润试题.files/image330.gif) 分别为:
分别为:
试题.files/image332.gif) 且
且试题.files/image334.gif) 2分
2分
试题.files/image336.gif)
所以试题.files/image338.gif) 5分
5分
(Ⅱ)因为试题.files/image340.gif) 所以
所以试题.files/image342.gif) 为增函数,
为增函数,
试题.files/image344.gif) ,所以
,所以试题.files/image346.gif) 时,生产A产品有最大利润为
时,生产A产品有最大利润为试题.files/image348.gif) (万美元)
(万美元)
又试题.files/image350.gif) ,所以
,所以试题.files/image352.gif) 时,生产B产品
时,生产B产品
有最大利润为460(万美元) 8分
现在我们研究生产哪种产品年利润最大,为此,我们作差比较:
试题.files/image354.gif) 10分
10分
所以:当试题.files/image356.gif) 时,投资生产A产品200件可获得最大年利润;
时,投资生产A产品200件可获得最大年利润;
当试题.files/image358.gif) 时,生产A产品与生产B产品均可获得最大年利润;
时,生产A产品与生产B产品均可获得最大年利润;
当试题.files/image360.gif) 时,投资生产B产品100件可获得最大年利润。12分
时,投资生产B产品100件可获得最大年利润。12分
19.解:(1)当试题.files/image362.gif) 时,
时,试题.files/image364.gif) ,
,试题.files/image366.gif) 成立,所以
成立,所以试题.files/image197.gif) 是偶函数;
是偶函数;
3分
当试题.files/image369.gif) 时,
时,试题.files/image371.gif) ,这时
,这时试题.files/image373.gif) 所以
所以试题.files/image197.gif) 是非奇非偶函数;
6分
是非奇非偶函数;
6分
(2)当试题.files/image199.gif) 时,
时,试题.files/image376.gif) 设
设试题.files/image378.gif) 且
且试题.files/image380.gif) ,则
,则
试题.files/image382.gif) 9分
9分
当试题.files/image378.gif) 时,因为
时,因为试题.files/image378.gif) 且
且试题.files/image380.gif) ,所以
,所以试题.files/image385.gif)
所以试题.files/image387.gif) ,
,
试题.files/image389.gif) ,所以
,所以试题.files/image197.gif) 是区间
是区间试题.files/image202.gif) 的单调递减函数。 14分
的单调递减函数。 14分
20.解:(Ⅰ)由抛物线试题.files/image218.gif) :
:试题.files/image394.gif) 知
知试题.files/image396.gif) ,设
,设试题.files/image398.gif) ,
,试题.files/image214.gif) 在
在试题.files/image218.gif) 上,且
上,且试题.files/image220.gif) ,所以
,所以试题.files/image403.gif) ,得
,得试题.files/image405.gif) ,代入
,代入试题.files/image394.gif) ,得
,得试题.files/image407.gif) ,
,
所以试题.files/image409.gif) 。
4分
。
4分
试题.files/image214.gif) 在
在试题.files/image216.gif) 上,由已知椭圆
上,由已知椭圆试题.files/image216.gif) 的半焦距
的半焦距试题.files/image414.gif) ,于是
,于是试题.files/image416.gif)
消去试题.files/image418.gif) 并整理得
并整理得 试题.files/image420.gif) , 解得
, 解得试题.files/image422.gif) (
(试题.files/image424.gif) 不合题意,舍去).
不合题意,舍去).
故椭圆试题.files/image216.gif) 的方程为
的方程为试题.files/image427.gif) 。
7分
。
7分
(另法:因为试题.files/image214.gif) 在
在试题.files/image216.gif) 上,
上,
所以试题.files/image429.gif) ,所以
,所以试题.files/image422.gif) ,以下略。)
,以下略。)
(Ⅱ)由试题.files/image432.gif) 得
得试题.files/image434.gif) ,所以点O到直线
,所以点O到直线试题.files/image436.gif) 的距离为
的距离为
试题.files/image438.gif) ,又
,又试题.files/image440.gif) ,
,
所以试题.files/image442.gif) ,
,
试题.files/image444.gif) 且
且试题.files/image446.gif) 。
10分
。
10分
下面视提出问题的质量而定:
如问题一:当试题.files/image227.gif) 面积为
面积为试题.files/image448.gif) 时,求直线
时,求直线试题.files/image436.gif) 的方程。(
的方程。(试题.files/image451.gif) ) 得2分
) 得2分
问题二:当试题.files/image227.gif) 面积取最大值时,求直线
面积取最大值时,求直线试题.files/image436.gif) 的方程。(
的方程。(试题.files/image453.gif) ) 得4分
) 得4分
21.解:(1)
试题.files/image240.gif)
2
3
35
100
试题.files/image242.gif)
97
94
3
1
4分
(2)试题.files/image455.gif) 由题意知数列
由题意知数列试题.files/image230.gif) 的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,
6分
的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,
6分
从而试题.files/image244.gif) =
=试题.files/image458.gif) 8分
8分
=试题.files/image460.gif) 10分
10分
(3)证明:①若试题.files/image462.gif) ,则题意成立,
12分
,则题意成立,
12分
②若试题.files/image464.gif) ,此时数列
,此时数列试题.files/image230.gif) 的前若干项满足
的前若干项满足试题.files/image466.gif) ,即
,即试题.files/image468.gif) ,
,
设试题.files/image470.gif) ,则当
,则当试题.files/image472.gif) 时,
时,试题.files/image474.gif) ,
,
从而此时命题成立; 14分
③若试题.files/image476.gif) ,由题意得
,由题意得试题.files/image478.gif) ,则由②的结论知此时命题也成立,
,则由②的结论知此时命题也成立,
综上所述,原命题成立。 16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com