
题目列表(包括答案和解析)
| m |
| n |
有甲、乙两种糖果,原价分别为每千克a元和b元.根据柜台组调查,将两种糖果按甲种糖果m千克与乙种糖果n千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨c%,乙种糖果单价下跌d%,但按原比例混合的糖果单价恰好不变,那么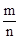 等于( )
等于( )
A.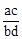 B.
B.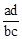 C.
C.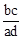 D.
D.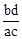
有甲、乙两种糖果,原价分别为每千克a元和b元.根据柜台组调查,将两种糖果按甲种糖果m千克与乙种糖果n千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨c%,乙种糖果单价下跌d%,但按原比例混合的糖果单价恰好不变,那么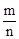 等于( )
等于( )
A.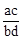 B.
B.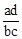 C.
C.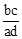 D.
D.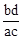
有甲、乙两种糖果,原价分别为每千克a元和b元.根据柜台组调查,将两种糖果按甲种糖果m千克与乙种糖果n千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨c%,乙种糖果单价下跌d%,但按原比例混合的糖果单价恰好不变,那么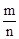 等于( )
等于( )
A.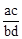 B.
B.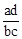 C.
C.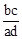 D.
D.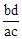
有甲、乙两种糖果,原价分别为每千克a元和b元.根据柜台组调查,将两种糖果按甲种糖果m千克与乙种糖果n千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价上涨c%,乙种糖果单价下跌d%,但按原比例混合的糖果单价恰好不变,那么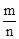 等于( )
等于( )
A.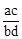 B.
B.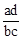 C.
C.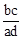 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com