
题目列表(包括答案和解析)
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±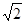
当y=4时,有x2-1=4,即x2=5
∴x=±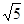
∴原方程的解为:x1=-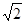 x2=
x2=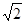 x3=-
x3=-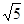 x4=
x4=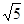
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程 -3(
-3(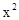 -3)=0
-3)=0
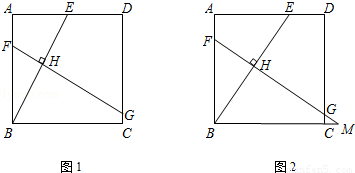
正方形ABCD中,E为AD上的一点(不与A、D点重合),AD=nAE,BE的垂直平分线分别交AB、CD于F、G两点,垂足为H.
(1)如图1,当n=2时,则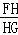 = _________ ;
= _________ ;
(2)如图1,当n=2时,求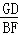 的值;
的值;
(3)延长FG交BC的延长线于M(如图2),直接填空:当n= _________ 时,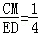 .
.


 x2=
x2= x3=-
x3=- x4=
x4=
 -3(
-3( -3)=0
-3)=0如图1,A,B,C为三个超市.在A通往C的道路(粗实线部分)上有一D点,D与B有道路(细实线部分)相通这.A与D,D与C,D与B之间的路程分别为25㎞,10㎞,5㎞.现计划在A通往C的道路上建一个配货中心H,每天有一辆货车只为这三个超市送货.该货车每于从H出发,单独为A送货1次,为B送货1次,为C送货2次.货车每次仅能给一家超市送货,每次送货后均返回配货中心H.设H到A的路程为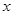 ㎞,这辆货车每天行驶的路程为
㎞,这辆货车每天行驶的路程为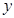 ㎞.
㎞.

(1)用含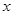 的代数式填空:当0≤
的代数式填空:当0≤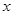 ≤25时货车从H到A往返1次的路程为2
≤25时货车从H到A往返1次的路程为2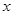 ㎞,货车从H到B往返1次的路程为 ㎞;货车从H到C往返2次的路程为 ㎞;这辆货车每天行驶的路程
㎞,货车从H到B往返1次的路程为 ㎞;货车从H到C往返2次的路程为 ㎞;这辆货车每天行驶的路程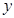 = ;当25<
= ;当25<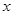 ≤35时,这辆货车每天行驶的路程
≤35时,这辆货车每天行驶的路程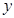 = ;
= ;
(2)请在图2中画出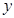 与
与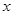 (0≤
(0≤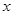 ≤35)的函数图象;
≤35)的函数图象;
(3)配货中心H建在哪段,这辆货车每天行驶的路程最短?
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±
当y=4时,有x2-1=4,即x2=5 ∴x=±
∴原方程的解为:x1=- x2=
x3=-
x4=
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程-3(
-3)=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com