
题目列表(包括答案和解析)
 仔细阅读并完成下题:
仔细阅读并完成下题:| 3 |
| 3 |
| 7 |
| 2 |
 (原创题)如图所示,平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一个动点.
(原创题)如图所示,平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一个动点.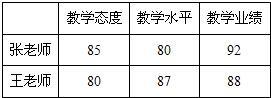 67、(原创题)某校为了对老师进行科学管理,建立了教师学期评分制度,其中,教学态度占20%,教学水平占20%,教学业绩占60%,以下是2008年秋季学期张老师,王老师的得分情况,则张老师的总评分为
67、(原创题)某校为了对老师进行科学管理,建立了教师学期评分制度,其中,教学态度占20%,教学水平占20%,教学业绩占60%,以下是2008年秋季学期张老师,王老师的得分情况,则张老师的总评分为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com