
题目列表(包括答案和解析)
| 5 |
| 5 |

| 5 |
| 5 |
| 5 |
| 5 |
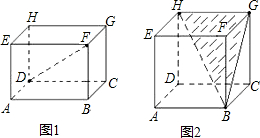 观察图(1),阅读理解关于长方体的对角线长定理:长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和.用符号表示即:DF2=FE2+FB2+FG2.应用这个定理尝试解决下列问题:已知图(2)是棱长为3cm的立方体,那么该立方体的对角线HB为
观察图(1),阅读理解关于长方体的对角线长定理:长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和.用符号表示即:DF2=FE2+FB2+FG2.应用这个定理尝试解决下列问题:已知图(2)是棱长为3cm的立方体,那么该立方体的对角线HB为 心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分). 心理学研究发现,一般情况下,在一节45分钟的课中,学生的活动随学习时间的变化而变化,开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生注意力开始分散,经过实验分析可知,学生的注意力指标数),随时间x(分钟)的变化规律如下图所示(其中AB、BC为线段,CD为双曲线的一部分).
心理学研究发现,一般情况下,在一节45分钟的课中,学生的活动随学习时间的变化而变化,开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生注意力开始分散,经过实验分析可知,学生的注意力指标数),随时间x(分钟)的变化规律如下图所示(其中AB、BC为线段,CD为双曲线的一部分). 需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com