
题目列表(包括答案和解析)
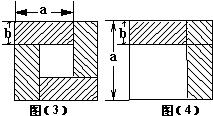 6、我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(3)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(4)面积的计算,验证了一个恒等式,此等式是( )
6、我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(3)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(4)面积的计算,验证了一个恒等式,此等式是( ) 我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图甲可以用来解释(a+b)2-(a-b)2=4ab.那么通过图乙面积的计算,验证了一个恒等式,此等式是( )
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图甲可以用来解释(a+b)2-(a-b)2=4ab.那么通过图乙面积的计算,验证了一个恒等式,此等式是( )我们已经学习了相似三角形,也知道,如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,是相似图形的有( )
A.①③ B.①② C.①④ D.②③
我们已经学习了相似三角形,也知道,如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,是相似图形的有( )
| A.①③ | B.①② | C.①④ | D.②③ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com