
题目列表(包括答案和解析)
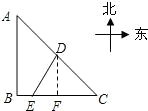 么相遇时补给船航行了多少海里?(结果精确到0.1海里,
么相遇时补给船航行了多少海里?(结果精确到0.1海里,| 6 |
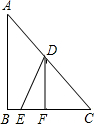 出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.| 6 |
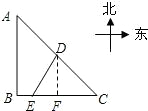 么相遇时补给船航行了多少海里?(结果精确到0.1海里,
么相遇时补给船航行了多少海里?(结果精确到0.1海里, ≈2.45)
≈2.45)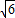 ≈2.45)
≈2.45)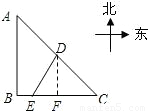
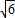 ≈2.45)
≈2.45)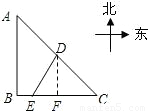
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com