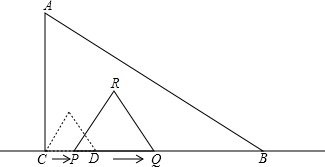
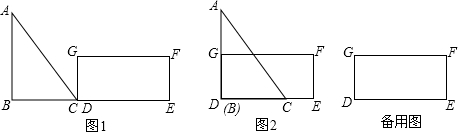
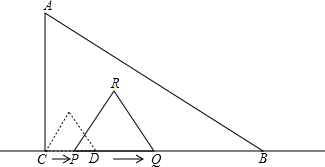
在Rt△ABC中,∠C=90°,BC=6cm,∠ABC=30°.D是CB上一点,DC=1cm.P、Q是直线CB上的两个动点,点P从C点出发,以1cm/s的速度沿直线CB向右运动,同时,点Q从D点出发,以2cm/s的速度沿直线CB向右运动,以PQ为一边在CB的上方作等边三角形PQR,如图是其运动过程中的某一位置.设运动的时间是t(s).
(1)△PQR的边长是
cm(用含有t的代数式表示);当t=
时,点R落在AB上.
(2)若等边△PQR与△ABC重叠部分的面积为y(cm
2),求y与t之间的函数关系式,并写出自变量t的取值范围.
(3)在P、Q移动的同时,以点A为圆心、tcm为半径的⊙A也在不断变化,请直接写出⊙A与△PQR的三边所在的直线相切时t的值.