
题目列表(包括答案和解析)

| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
近年来,万州区教委在九年义务教育阶段实施“变革课堂”改革实验,推动高效卓越课堂,让学生在课堂教学中体验自主学习、合作探究、共同进步的教育理念,营造宽松、民主、活跃的生态课堂,成绩显著.不少学校真正体现了学生成为学习的主体,教师为主导的学习过程,某校八年级为了解学生课堂发言情况,对该年级部分学生某一天在课堂上发言的次数进行了抽查统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图.已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题: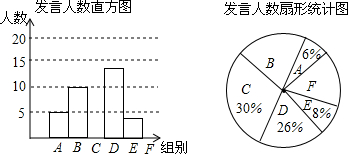
(1)根据给定条件直接写出B组发言人数是多少?
(2)求C组的发言人数,补全直方图;
(3)该年级共有学生500人,请估计全年级在这一天里发言次数不少于12次的人数.
| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |

 1、下面的扇形统计图反映了七(1)班学生在课外活动中参加各小组的情况,看图回答:
1、下面的扇形统计图反映了七(1)班学生在课外活动中参加各小组的情况,看图回答:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com