
题目列表(包括答案和解析)
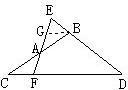 13、如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B,与DF的延长线交于点C,且BE=CF.
13、如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B,与DF的延长线交于点C,且BE=CF.| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
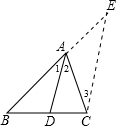 E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明| BD |
| DC |
| AB |
| AC |
|
|
| BD |
| DC |
| AB |
| AC |
 []
[]已知矩形 和点
和点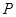 ,当点
,当点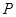 在图
在图 中的位置时,求证:
中的位置时,求证: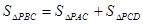
证明:过点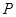 作
作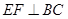 交
交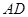 、
、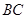 于
于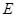 、
、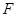 两点,
两点,
∵ 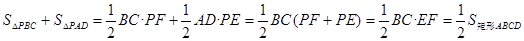
又∵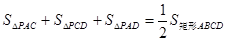
∴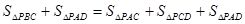 ,∴
,∴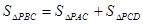
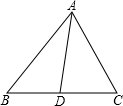
请你参考上述信息,当点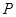 分别在图
分别在图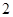 、图
、图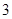 中的位置时,请你分别写出
中的位置时,请你分别写出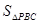 、
、 、
、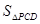 之间的数量关系?,并选择其中一种情况给予证明
之间的数量关系?,并选择其中一种情况给予证明
观察计算:
当 ,
,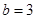 时,
时,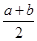 与
与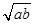 的大小关系是_________________.
的大小关系是_________________.
当 ,
, 时,
时,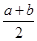 与
与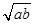 的大小关系是_________________.
的大小关系是_________________.
探究证明:
如图所示, 为圆O的内接三角形,
为圆O的内接三角形,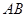 为直径,过C作
为直径,过C作 于D,设
于D,设 ,BD=b.
,BD=b.

(1)分别用 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得出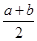 与
与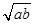 的大小关系是:______________.
的大小关系是:______________.
实践应用:
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
如图①所示,已知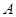 、
、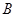 为直线
为直线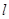 上两点,点
上两点,点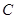 为直线
为直线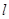 上方一动点,连接
上方一动点,连接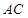 、
、 ,分别以
,分别以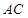 、
、 为边向
为边向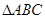 外作正方形
外作正方形 和正方形
和正方形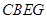 ,过点
,过点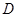 作
作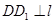 于点
于点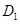 ,过点
,过点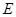 作
作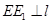 于点
于点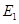 .
.
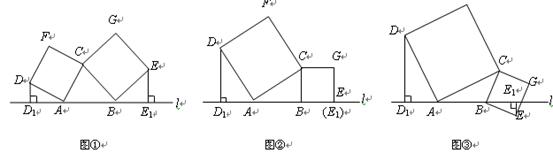
(1)如图②,当点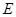 恰好在直线
恰好在直线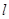 上时(此时
上时(此时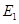 与
与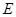 重合),试说明
重合),试说明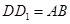 ;
;
(2)在图①中,当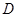 、
、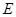 两点都在直线
两点都在直线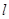 的上方时,试探求三条线段
的上方时,试探求三条线段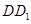 、
、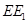 、
、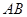 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)如图③,当点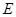 在直线
在直线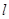 的下方时,请直接写出三条线段
的下方时,请直接写出三条线段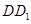 、
、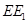 、
、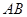 之间的数量关系.(不需要证明)
之间的数量关系.(不需要证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com