
题目列表(包括答案和解析)
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图①,求证:MN2=AM2+BN2;
思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.
请你完成证明过程:

(Ⅱ)当扇形CEF绕点C旋转至图②的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.

如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.

(1)求证:点E是边BC的中点;
(2)若EC=3,BD=2![]() ,求⊙O的直径AC的长度;
,求⊙O的直径AC的长度;
(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
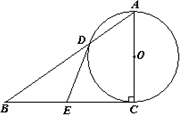
(1)求证:点E是边BC的中点;
(2)若EC=3,BD=![]() ,求⊙O的直径AC的长度;
,求⊙O的直径AC的长度;
(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
如图,在直角三角形ABC中,∠ABC=90°.
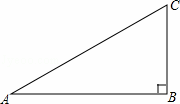
(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=![]() ,sinA=
,sinA=![]() ,求△AOC的面积.
,求△AOC的面积.
如图,在平面直角坐标系中,抛物线![]() 相交于A,B两点.
相交于A,B两点.
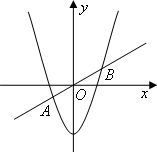
(1)求线段AB的长.
(2)若一个扇形的周长等于(1)中线段AB的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少?
(3)如图,线段AB的垂直平分线分别交x轴、y轴于C,D两点,垂足为点M,分别求出OM,OC,OD的长,并验证等式![]() 是否成立.
是否成立.

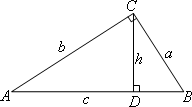
(4)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,设BC=a,AC=b,AB=c.CD=b,试说明:![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com