
题目列表(包括答案和解析)
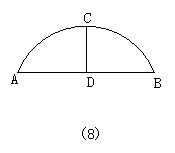
如图8所示,已知有一圆形桥拱,拱的跨度AB=16cm,拱高CD=4cm,那么拱形的半径是________cm.
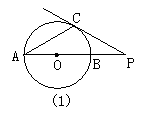
如图1所示,已知⊙O的直径AB与弦AC夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为( )
A.![]() ; B.
; B.![]() C.10 D.5
C.10 D.5
如图4所示,已知![]() 直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.
直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.

某水电站的蓄水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.已知某天0点到6点,进行机组试运行,试机时至少打开一个水口,且该水池的蓄水量与时间的关系如图丙所示:给出以下3个判断:①0点到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水不出水. 则上述判断中一定正确的是( )
A、① B、② C、②③ D、①②③
B、
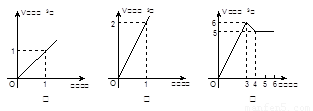
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com