证明:∵AB=AC,∴∠ABC=∠ACB, ∵CE.BD是高, ∴∠CEB=∠BDC=90°, 在△CEB和△BDC中,∠EBC=∠DCB,∠CEB=∠BDC,BC=CB, ∴△CEB≌△BD——青夏教育精英家教网—

证明:∵AB=AC,∴∠ABC=∠ACB, ∵CE.BD是高, ∴∠CEB=∠BDC=90°, 在△CEB和△BDC中,∠EBC=∠DCB,∠CEB=∠BDC,BC=CB, ∴△CEB≌△BDC, ∴CE=BD. 【查看更多】

题目列表(包括答案和解析)

如图，已知△ABC中，AB=AC，点D、E分别在AB、AC上，且BD=CE，如何说明OB=OC呢？

解：∵AB=AC
∴∠ABC =∠ACB （      ）
又∵BD=CE （      ）
BC=CB （       ）
∴△BCD≌△CBE （     ）
∴∠（）= ∠（）
∴OB = OC （      ）。

查看答案和解析>>

黄金分割比是生活中比较多见的一种长度比值，它能给人许多美感和科学性，我们初中阶段学过的许多几何图形也有着类似的边长比例关系．例如我们熟悉的顶角是36°的等腰三角形，其底与腰之比就为黄金分割比

-1

，底角平分线与腰的交点为黄金分割点．
（1）如图1，在△ABC中，∠A=36°，AB=AC，∠ACB的角平分线CD交腰AB于点D，请你证明点D是腰AB的黄金分割点；
（2）如图2，在△ABC中，AB=AC，若

-1

，则请你求出∠A的度数；
（3）如图3，如果在Rt△ABC中，∠ACB=90°，CD为AB上的高，∠A、∠B、∠ACB的对边分别为a，b，c．若点D是AB的黄金分割点，那么该直角三角形的三边a，b，c之间是什么数量关系？并证明你的结论．

查看答案和解析>>

如图，B、D、C、F四点在同一条直线上，BD=CF，AC∥ED，AC=ED．请补充完整证明“AB∥EF”的推理过程．

证明：∵AC∥ED
∴∠ACB=∠EDF（

两直线平行，内错角相等

）
∵BD=FC
∴BD+CD=FC+CD
即BC=FD
在△ABC与△EFD中
∵（

AC=DE，∠ACB=∠EDF，BC=DF

）
∴△ABC≌△EFD（

SAS

）
∴

∠B=∠F

（

全等三角形的对应角相等

）
∴AB∥EF（

内错角相等，两直线平行

）

查看答案和解析>>

我们知道：将一条线段AB分割成大小两条线段AC、CB，若小线段CB与大线段AC的长度之比等于大线段AC与线段AB的长度之比，即

-1

=0.61803398874989．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．
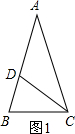
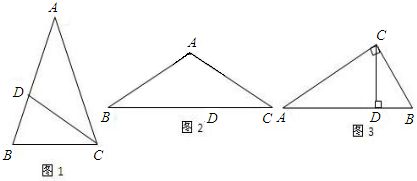
（1）如图1，在△ABC中，∠A=36°，AB=AC，∠ACB的角平分线CD交腰AB于点D，请你说明D为腰AB的黄金分割点的理由．
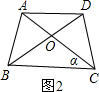
（2）若腰和上底相等，对角线和下底相等的等腰梯形叫作黄金梯形，其对角线的交点为对角线的黄金分割点．如图2，AD‖BC，AB=AD=DC，AC=BD=BC，试说明O为AC的黄金分割点．
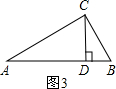
（3）如图3，在Rt△ABC中，∠ACB=90°，CD为斜边AB上的高，∠A、∠B、∠ACB的对边分别为a、b、c．若D是AB的黄金分割点，那么a、b、c之间的数量关系是什么并证明你的结论．

查看答案和解析>>

28、在△ABC中，AB=AC，∠ACB=∠ABC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．
（1）在图1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；
（2）当三角尺沿AC方向平移到图2所在的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE、DF与CG之间满足的数量关系，然后证明你的猜想；（提示：过点D作DH⊥CG，可得四边形EDHG是长方形）
（3）当三角尺在（2）的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，试猜想DE，DF与CG之间满足的数量关系．（不用说明理由）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学