
题目列表(包括答案和解析)
| 2 |
| 2 |
| 3 |
| n |
 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题:
 (2012•郴州)如图,D、E分别是△ABC的边AB、AC上的点,连接DE,要使△ADE∽△ACB,还需添加一个条件
(2012•郴州)如图,D、E分别是△ABC的边AB、AC上的点,连接DE,要使△ADE∽△ACB,还需添加一个条件 bx+c=0的两个根满足|x1-x2|=
bx+c=0的两个根满足|x1-x2|=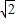 ,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.
,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.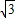 bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;
bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;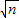 bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由)
bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com