
题目列表(包括答案和解析)
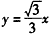 上,AB边在直线
上,AB边在直线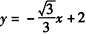 上。
上。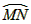 ,分别交边OA、OC 于M、N(M、N可以与A、C重合),作⊙Q与边AB、BC和
,分别交边OA、OC 于M、N(M、N可以与A、C重合),作⊙Q与边AB、BC和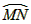 都相切,⊙Q分别与边AB、BC相切于点D、E,设⊙Q的半径为r,OP的长为y,求y与r 之间的函数关系式,并写出自变量r的取值范围;
都相切,⊙Q分别与边AB、BC相切于点D、E,设⊙Q的半径为r,OP的长为y,求y与r 之间的函数关系式,并写出自变量r的取值范围;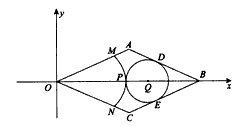
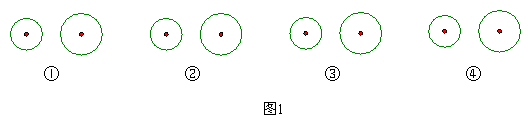
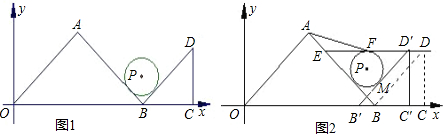
(1)如图1,请你类比直线和一个圆的三种位置关系,在图1的①、②、③中,分别各画出一条直线,使它与两个圆都相离、与两个圆都相切、与一个圆相离且与另一个圆相交,并在图1的④中也画上一条直线,使它与两个圆具有不同于前面3种情况的位置关系;
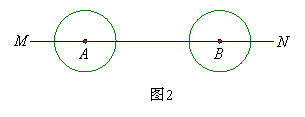
(2)如图2,点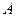 、
、 在直线MN上,AB=11厘米,
在直线MN上,AB=11厘米, 、
、 的半径均为1厘米.
的半径均为1厘米. 以每秒2厘米的速度自左向右运动,与此同时,
以每秒2厘米的速度自左向右运动,与此同时, 的半径
的半径 也不断增大,其半径
也不断增大,其半径 (厘米)与时间t(秒)之间的关系式为
(厘米)与时间t(秒)之间的关系式为  .请直接写出点
.请直接写出点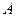 出发后多少秒两圆内切?
出发后多少秒两圆内切?
(1)如图1,请你类比直线和一个圆的三种位置关系,在图1的①、②、③中,分别各画出一条直线,使它与两个圆都相离、与两个圆都相切、与一个圆相离且与另一个圆相交,并在图1的④中也画上一条直线,使它与两个圆具有不同于前面3种情况的位置关系;
(2)如图2,点![]() 、
、![]() 在直线MN上,AB=11厘米,
在直线MN上,AB=11厘米,![]() 、
、![]() 的半径均为1厘米.
的半径均为1厘米.![]() 以每秒2厘米的速度自左向右运动,与此同时,
以每秒2厘米的速度自左向右运动,与此同时,![]() 的半径也不断增大,其半径
的半径也不断增大,其半径![]() (厘米)与时间t(秒)之间的关系式为
(厘米)与时间t(秒)之间的关系式为 ![]() .请直接写出点
.请直接写出点![]() 出发后多少秒两圆内切?
出发后多少秒两圆内切?
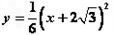 的图像的顶点为A,与y轴交于点B,以AB为边在第二象限内作等边三角形ABC.
的图像的顶点为A,与y轴交于点B,以AB为边在第二象限内作等边三角形ABC.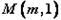 在第二象限,且△ABM的面积等于△ABC的面积,求点M的坐标.
在第二象限,且△ABM的面积等于△ABC的面积,求点M的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com