
题目列表(包括答案和解析)
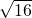 的算术平方根是4
的算术平方根是4 的算术平方根是4
的算术平方根是4  的两根之和是-5
的两根之和是-5 如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.

(1)求证:PB是⊙O的切线;
(2)求证: AQ·PQ= OQ·BQ;
(3)设∠AOQ=.若cos
=
.OQ= 15.求AB的长
【解析】此题考核圆的切线,相似三角形的判定和性质
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.

(1)求证:PB是⊙O的切线;
(2)求证: AQ·PQ= OQ·BQ;
(3)设∠AOQ= .若cos
.若cos =
= .OQ= 15.求AB的长
.OQ= 15.求AB的长
【解析】此题考核圆的切线,相似三角形的判定和性质
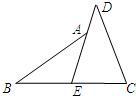 31、阅读下面的题目及分析过程,并按要求进行证明.
31、阅读下面的题目及分析过程,并按要求进行证明.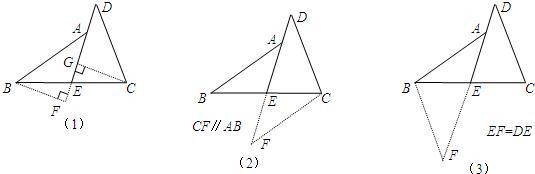
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com