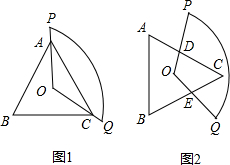
O是边长为a的正多边形的中心,将一块半径足够长,圆心角为α的扇形纸板的圆心放在O点处,并将纸板绕O点旋转.
(1)若正多边形为正三角形,扇形的圆心角α=120°,请你通过观察或测量,填空:
①如图1,正三角形ABC的边被扇形纸板覆盖部分的总长度为
;
②如图2,正三角形ABC的边被扇形纸板覆盖部分的总长度为
;
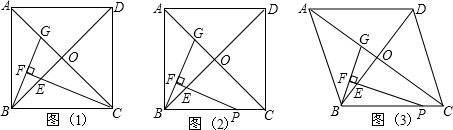
(2)若正多边形为正方形,扇形的圆心角α=90°时,①如图3,正方形ABCD的边被扇形纸板覆盖部分的总长度为
;
②如图4,正方形ABCD的边被扇形纸板覆盖部分的总长度为多少?并给予证明;
(3)若正多边形为正五边形,如图5,当扇形纸板的圆心角α为
时,正五边形的边被扇形纸板覆盖部分的总长度仍为定值a.
(4)一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处,并将纸板绕O点旋转.当扇形纸板的圆心角为
时,正n边形的边被扇形纸板覆盖部分的总长度为定值a.