数学课堂上,徐老师出示一道试题:
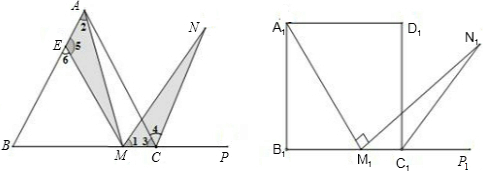
如图1所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连接EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=
∠ACP=60°.∴∠MCN=∠3+∠4=120°…①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.…②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
.
∴△AEM≌△MCN (ASA).∴AM=MN.
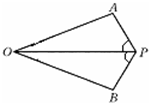
(2)若将试题中的“正三角形ABC”改为“正方形A
1B
1C
1D
1”(如图2),N
1是∠D
1C
1P
1的平分线上一点,则当∠A
1M
1N
1=90°时,结论A
1M
1=M
1N
1.是否还成立?(直接写出答案,不需要证明)
(3)若将题中的“正三角形ABC”改为“正多边形A
nB
nC
nD
n…X
n”,请你猜想:当∠A
nM
nN
n=
°时,结论A
nM
n=M
nN
n仍然成立?(直接写出答案,不需要证明)

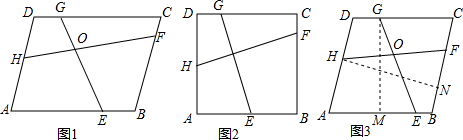
 19、如图,已知∠APO=∠BPO,∠A=∠B,说明△AOP≌△BOP.
19、如图,已知∠APO=∠BPO,∠A=∠B,说明△AOP≌△BOP.
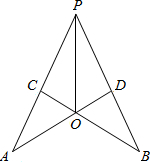 阅读下题的两个解答过程,然后回答问题:
阅读下题的两个解答过程,然后回答问题: