练习册

  • 练习册
  • 试题
    (二) 11.证法一:如答图1所示,过C作CD∥AB,∴∠B=∠BCD,∵AB∥EF,CD∥AB, ∴CD∥EF,∴∠F=∠DCF,∴∠BCD+∠DCF=∠B+∠F,即∠BCF=∠B+∠F. 证法二:如答图2所示,过C作DC∥AB,∴∠B+∠BCD=180°, ∵AB∥EF,DC ∥AB, ∴DC∥EF,∴∠DCF+∠F=180°,∴∠B+∠BCD+∠DCF+∠F=360°, ∴∠B+∠F=360°-=∠BCF,即∠BCF=∠B+∠F. 证法三:如答图3所示,延长BC交EF于D,∵AB∥EF,∴∠CDF=∠B, ∵∠BCF=∠CDF+ ∠F,∴∠BCF=∠B+∠F. 证法四:如答图4所示,连结BF,∵AB∥EF, ∴∠ABF+∠EFB=180°, 即∠ABC+∠CBF+∠BFC+∠CFE=180°, ∴∠ABC+∠CFE=180°-= ∠BCF, 即∠BCF= ∠ABC+∠EFC. 证法五:如答图5所示,过B作CF的平行线,交EF的延长线于D, ∵AB∥EF,∴∠GBA= ∠D.∵BD∥CF,∴∠CFE=∠D, ∴∠GBA=∠CFE,BD∥CF, ∴∠BCF=∠CBG=∠ABC+∠GBA=∠ABC+∠CFE,即∠BCF=∠ABC+∠CFE. 12.证法一:如图1所示,作BC的延长线CD,在△ABC的外部,以CA为一边,CE 为一边画∠1=∠A,∴CE∥BA,∴∠B=∠2.∵∠1+∠2+∠ACB=180°,∴∠A+∠B+∠ACB=180° 证法二:如答图2所示,过A作BC的平行线DE,∴∠B=∠DAB,∠C=∠EAC. ∵∠DAB+∠BAC+∠EAC=180°,∴∠BAC+∠B+∠C=180°. 证法三:如答图3所示,过B作CA的平行线DB, 则有∠DBA=∠A,∠DBA+ ∠ABC+ ∠C=180°.∴∠A+∠ABC+∠C=180°. 证法四:如答图4所示,在BC上取一点D,过D分别作AB.AC的平行线交AC.AB于E.F,则有四边形AFDE为平行四边形,所以∠FDE=∠A,∠EDC=∠B,∠FDB=∠C. ∵∠EDC+ ∠FDE+∠FDB=180°,∴∠A+∠B+∠C=180°. 【查看更多】

     

    题目列表(包括答案和解析)

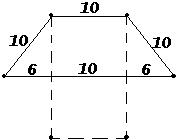    10、墙上钉着用一根彩绳围成的梯形形状的饰物，如右图实线所示．小颖将梯形下底的钉子去掉，并将这条彩绳钉成一个长方形，如右图虚线所示．小颖所钉长方形的长、宽各为多少厘米？

    查看答案和解析>>

    挪杯子：有6只玻璃杯并排放在一起，左边三只盛满水，右边3只是空的，如右图a所示的状态，现要摆成如图b所示的状态．如果一次只能移动一只杯子，请问至少要挪动多少次？（限时：2分钟）

    查看答案和解析>>

    如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是多少?

     

    查看答案和解析>>

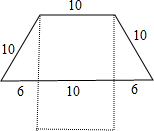    墙上钉着用一根彩绳围成的梯形形状的饰物，如右图实线所示．小颖将梯形下底的钉子去掉，并将这条彩绳钉成一个长方形，如右图虚线所示．小颖所钉长方形的长、宽各为多少厘米？

    查看答案和解析>>

    已知二次函数y=ax2+bx+c(a≠0)的图象如右图的所示,则下列结论：

    ①a-b+c>o，

    ②方程ax2+bx+c=0的两根之和大于零；

    ③y随x的增大而增大；

    ④一次函数y=ax+bc的图象一定不过第二象限．

    其中正确的个数是  (   )

    A．1个    B．2个    C．3个    D．4个

    查看答案和解析>>


    同步练习册答案