
题目列表(包括答案和解析)
| A、正五边形 | B、正六边形 | C、正三角形 | D、正四边形 |
| ||
| 4 |
| ||
| 4 |
| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
| A、每个内角都是120°的六边形一定是正六边形 | B、正n边形有n条对称轴 | C、正n边形的每一个外角度数等于它的中心角度数的二倍 | D、正多边形一定既是轴对称图形,又是中心对称图形 |
已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是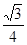 ,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)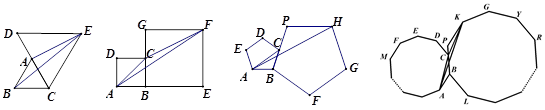
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com