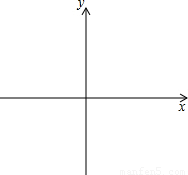
(2013•宜兴市一模)如图1,正方形ABCD的边长为a(a为常数),对角线AC、BD相交于点O,将正方形KPMN(KN>
AC)的顶点K与点O重合,若绕点K旋转正方形KPMN,不难得出,两个正方形重合部分的面积始终是正方形ABCD面积的四分之一.
(1)①在旋转过程中,正方形ABCD的边被正方形KPMN覆盖部分总长度是定值吗?如果是,请求出这个定值,如果不是,请说明理由.
②如图2,若将上题中正方形ABCD改为正n边形,正方形KPMN改为半径足够长的扇形,并将扇形的圆心绕点O旋转,设正n边形的边长为a,面积为S,当扇形的圆心角为
°时,两个图形重合部分的面积是
,这时正n边形的边被扇形覆盖部分的总长度为
a
a
.
(2)如图3,在正方形KNMP旋转过程中,记KP与AD的交点为E,KN与CD的交点为F.连接EF,令AE=x,S
△OEF=S,当正方形ABCD的边长为2时,试写出S关于x的函数关系式,并求出x为何值时S取最值,最值是多少.
(3)若将这两张正方形按如图4所示方式叠放,使K点与CD的中点E重合(AB≤
),正方形ABCD以1cm/s的速度沿射线KM运动,当正方形ABCD完全进入正方形KPMN时即停止运动,正方形ABCD的边长为8cm,且CD⊥KM,求两正方形重叠部分面积y与运动时间t之间的函数关系式.

 于点C,顶点为P,此抛物线的对称轴为直线x=1,且S△AOC:S△BOC=1:3.
于点C,顶点为P,此抛物线的对称轴为直线x=1,且S△AOC:S△BOC=1:3. 于点C,顶点为P,此抛物线的对称轴为直线x=1,且S△AOC:S△BOC=1:3.
于点C,顶点为P,此抛物线的对称轴为直线x=1,且S△AOC:S△BOC=1:3.