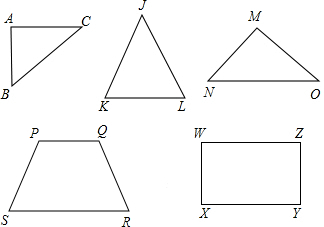
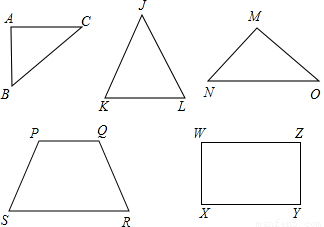
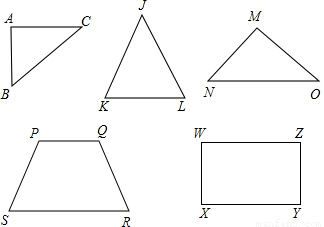
有如图所示的五种塑料薄板(厚度不计):①两直角边分别为3、4的直角三角形ABC;
②腰长为4、顶角为36°的等腰三角形JKL;
③腰长为5、顶角为120°的等腰三角形OMN;
④两对角线和一边长都是4且另三边长相等的凸四边形PQRS;
⑤长为4且宽(小于长)与长的比是黄金分割比的黄金矩形WXYZ.
它们都不能折叠,现在将它们一一穿过一个内、外径分别为2.4、2.7的铁圆环.
我们规定:如果塑料板能穿过铁环内圈,则称为此板“可操作”;否则,便称为“不可操作”.
(1)证明:第④种塑料板“可操作”;求:从这五种塑料板中任意取两种至少有一种“不可操作”的概率.