
题目列表(包括答案和解析)
| nπR2 |
| 360 |
| nπR |
| 180 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
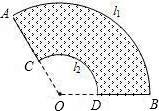
 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l= ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
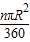 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l=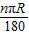 ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.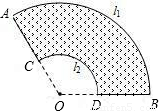
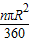 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l=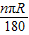 ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.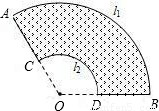
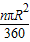 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l=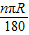 ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.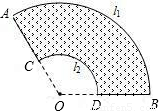
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com