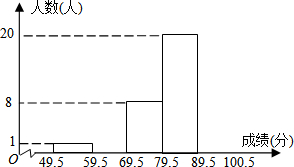（2013•湖州二模）某校为了了解学生对文明礼仪的知晓程度，从全校1200名学生中随机抽取了50名学生进行测试．根据测试成绩（成绩取整数，满分为100分）作了统计分析，绘制成频数分布直方图（如图，其中部分数据缺失）．又知90分以上（含90分）的人数比60～70分（含60分，不含70分）的人数的2倍还多3人．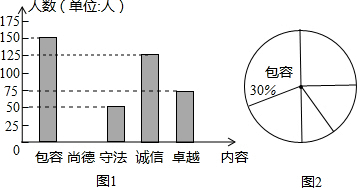
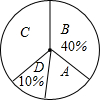请你根据上述信息，解答下列问题：
（1）该统计分析的样本是．
A、1200名学生；                        B、被抽取的50名学生；
C、被抽取的50名学生的问卷成绩；        D、50
（2）被测学生中，成绩不低于90分的有多少人？
（3）测试成绩的中位数所在的范围是．
（4）如果把测试成绩不低于80分记为优良，试估计该校有多少名学生对文明礼仪的知晓程度达到优良．

（2012•山西）今年太原市提出城市核心价值观：“包容、尚德、守法、诚信、卓越”．某校德育处为了了解学生对城市核心价值观中哪一项内容最感兴趣，随机抽取了部分学生进行调查，并将调查结果绘成如图统计图．请你结合图中信息解答下列问题：

（1）填空：该校共调查了名学生．
（2）请你分别把条形统计图和扇形统计图补充完整．

（2012•和平区二模）某校为了了解学生对交通安全知识掌握情况，在学校随机抽取了部分学生进行了交通安全知识测试．成绩按A（优秀）、B（良好）、C（合格）、D（不合格）四个等级进行统计，并将统计结果绘制成如下不完整的统计图表．请结合图表中所给信息解答下列问题：
（1）将表格中缺少的数据补充完整；
（2）扇形统计图中“A”部分所对应的圆心角的度数是°．“C”部分所占百分比是；
（3）若该校共有1650名学生，试估计交通安全知识测试成绩合格以上（含合格）的人数．

等级	A（优秀）	B（良好）	C（合格）	D（不合格）
人数（人）	45	120	105	30 30

（2013•牡丹江）某校为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取了本校部分学生进行问卷调查（必选且只选一类节目），将调查结果进行整理后，绘制了如下不完整的条形统计图和扇形统计图，其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人．

请根据所给信息解答下列问题：
（1）求本次抽取的学生人数．
（2）补全条形图，在扇形统计图中的横线上填上正确的数值，并直接写出“体育”对应的扇形圆心角的度数．
（3）该校有3000名学生，求该校喜爱娱乐节目的学生大约有多少人？

太仓人杰地灵，为了了解学生对家乡历史文化名人的知晓情况，某校对部分学生进行了随机抽样调查，并将调查结果绘制成如图所示统计图的一部分．

根据统计图中的信息，回答下列问题：
（1）本次抽样调查的样本容量是；
（2）在扇形统计图中，“了解很少”所在扇形的圆心角是度；
（3）若全校共有学生1300人，那么该校约有多少名学生“基本了解”太仓的历史文化名人？