
题目列表(包括答案和解析)
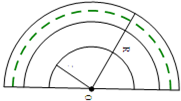 在一场篮球比赛中,一球星将球出手时,球离地面
在一场篮球比赛中,一球星将球出手时,球离地面 米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.
米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米. ),球运行的最高点坐标为(4,4),求出此坐标系中球的运行轨迹抛物线对应的函数关系式(不要求写取值范围);
),球运行的最高点坐标为(4,4),求出此坐标系中球的运行轨迹抛物线对应的函数关系式(不要求写取值范围);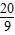 米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.
米,球的运行轨迹为抛物线,当球运行的水平距离为4米时,球到达的最高点离地4米.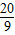 ),球运行的最高点坐标为(4,4),求出此坐标系中球的运行轨迹抛物线对应的函数关系式(不要求写取值范围);
),球运行的最高点坐标为(4,4),求出此坐标系中球的运行轨迹抛物线对应的函数关系式(不要求写取值范围);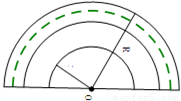
 在一场篮球比赛中,一球星将球出手时,球离地面
在一场篮球比赛中,一球星将球出手时,球离地面| 20 |
| 9 |
| 20 |
| 9 |
 永嘉县九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
永嘉县九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高| 20 | 9 |
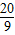 m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,建立如图的平面直角坐标系,设篮球出手后离地的水平距离为xm,高度为ym,则y关于x的函数解析式是 .
m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,建立如图的平面直角坐标系,设篮球出手后离地的水平距离为xm,高度为ym,则y关于x的函数解析式是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com