
题目列表(包括答案和解析)

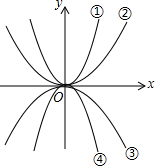 如图所示,四个函数图象对应的解析式分别是:①y=ax2,②y=bx2,③y=cx2,④y=dx2,则a,b,c,d的大小关系是
如图所示,四个函数图象对应的解析式分别是:①y=ax2,②y=bx2,③y=cx2,④y=dx2,则a,b,c,d的大小关系是
|
|
| 1 |
| x |
| x+1 |
| x |
| 1 |
| x |
| x-1 |
| x-2 |
| x+b |
| x+a |
 的图象向右平移1个单位,所得图象的函数表达式为______,再向上平移1个单位,所得图象的函数表达式为______;
的图象向右平移1个单位,所得图象的函数表达式为______,再向上平移1个单位,所得图象的函数表达式为______; 的图象可由
的图象可由 的图象向______平移______个单位得到;
的图象向______平移______个单位得到; 的图象可由哪个反比例函数的图象经过怎样的变换得到
的图象可由哪个反比例函数的图象经过怎样的变换得到 (ab≠0,且a≠b)可由哪个反比例函数的图象经过怎样的变换得到.
(ab≠0,且a≠b)可由哪个反比例函数的图象经过怎样的变换得到.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com