
题目列表(包括答案和解析)
在平面直角坐标系xOy中,如图,将若干个边长为 的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.
的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.
(1)如图,当正方形个数为1时,填空:点B′坐标为 ,点C′坐标为 ,二次函数的关系式为 ,此时抛物线的对称轴方程为 ;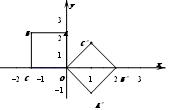
(2)如图,当正方形个数为2时,求y=ax2+bx+c(a≠0)图像的对称轴;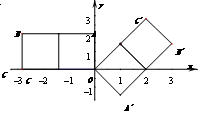
(3)当正方形个数为2013时,求y=ax2+bx+c(a≠0)图像的对称轴;
(4)当正方形个数为n个时,请直接写出:用含n的代数式来表示y=ax2+bx+c(a≠0)图像的对称轴。
已知二次函数y=ax2+bx+c的图象如图所示,
下列结论:①a+b+c<0②a-b+c>0 ③abc>0
④b=2a其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
已知二次函数y=ax2+bx+c的图象如图所示,
下列结论:①a+b+c<0 ②a-b+c>0 ③abc>0
④b=2a其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:① a+b+c<0;② a-b+c<0;③ b+2a<0;④ abc>0 .其中所有正确结论的序号是( )
| A.③④ | B.②③ | C.①④ | D.①②③ |
在平面直角坐标系xOy中,如图,将若干个边长为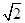 的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.
的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.
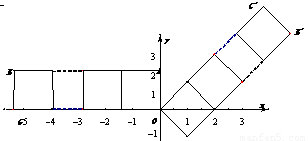
(1)如图,当正方形个数为1时,填空:点B′坐标为 ,点C′坐标为 ,二次函数的关系式为 ,此时抛物线的对称轴方程为 ;
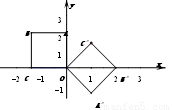
(2)如图,当正方形个数为2时,求y=ax2+bx+c(a≠0)图像的对称轴;

(3)当正方形个数为2013时,求y=ax2+bx+c(a≠0)图像的对称轴;
(4)当正方形个数为n个时,请直接写出:用含n的代数式来表示y=ax2+bx+c(a≠0)图像的对称轴。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com