
题目列表(包括答案和解析)
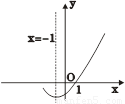
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.
其中正确的命题是: .(只要求填写正确命题的序号)
在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.
(1)①列车已行驶的路程s(km)与行驶的时间t(h)的函数关系式是s=300t,该函数的平均变化率是 ;其蕴含的实际意义是 ;
②飞机着陆后滑行的距离y(m)与滑行的时间x(s)的函数关系式是y=-1.5x2+60x,求该函数的平均变化率;
(2)通过比较(1)中不同函数的平均变化率,你有什么发现;
(3)如图,二次函数y=ax2+bx+c的图像经过第一象限内的三点A、B、C,过点A、B、C作x轴的垂线,垂足分别为D、E、F,AM⊥BE,垂足为M,BN⊥CF,垂足为N,DE=EF,试探究△AMB与△BNC面积的大小关系,并说明理由.
已知反比例函数y= 的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
(1)求a的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,请说明理由.
如图,已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于 A(-2,4)、B(8,2)两点,则能使关于x的不等式 ax2+(b-k)x+c-m>0 成立的x的取值范围是______.

今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
|
周数x |
1 |
2 |
3 |
4 |
|
价格y(元/千克) |
2 |
2.2 |
2.4 |
2.6 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式;
(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=x+1.2,5月份此种蔬
菜的进价m(元/千克)与周数x所满足的函数关系为m=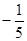 x+2.试问4月份与5月份分别在哪一周销
x+2.试问4月份与5月份分别在哪一周销
售此种蔬菜一千克的利润最大?且最大利润分别是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com