
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
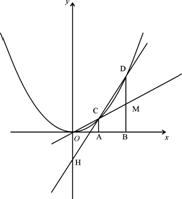
如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。记C、D的横坐标分别为xC,xD,点H的纵坐标yH。
(1)证明:①S△CMD∶S梯形ABMC=2∶3
②xC·xD=-yH
(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。记C、D的横坐标分别为xC,xD,点H的纵坐标yH。
(1)证明:①S△CMD∶S梯形ABMC=2∶3
②xC·xD=-yH
(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
 (3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
关于二次函数y=2x2+3,下列说法中正确的是 ( )
A.它的开口方向是向下 B.当x<-1时,y随x的增大而减小
C.它的顶点坐标是(2,3) D.当x=0时,y有最大值是3
二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com