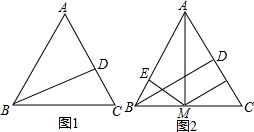
（2013•莒南县一模）【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．（无需证明）
【拓展变式】小明很顺利的完成了上面的练习后，又进一步对该命题进行了发散思维，把原命题中的一些条件进行了变换，得到了如下三个不同的命题：
（1）如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．
（2）如果两个三角形有两条边和第三边上的高对应相等，那么这两个三角形全等．
（3）如果两个三角形有两条边和夹角的平分线对应相等，那么这两个三角形全等．
【探索新知】小明对这三个命题，无法判断其命题的真假，于是他向老师求教．数学老师对命题（1）做出了一些指导，请你帮助小明完成下面的解答过程．
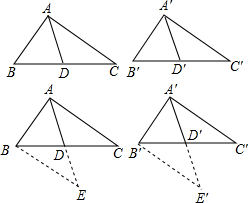
已知：如图，AB=A′B′，AD=A′D′，AD是BC边上的中线，A′D′是B′C′边上的中线，求证：△ABC≌△A′B′C′，
证明：如图，延长AD至E使AD=DE，连接BE，延长A′D′至E′使A′D′=D′E′，连接B′E′．
【合作学习】对于命题（2）、（3），你能帮助小明判断命题的真假吗？如果是真命题，请给完整的证明，如果是假命题，在下面的空白处做出解答．（要求：画出图形，说明理由．）

一次数学合作学习活动中，明明提出这样三个问题，请你帮他解决：
(1)把正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起，其中∠PAQ=90 °。点Q在边BC上，连接PD，△ADP与△ABQ全等吗？请说明理由。
(2)如图2，O为正方形ABCD对角线的交点，将一直角三角板FPQ的直角顶点 F与点O重合, 转动三角板使两直角边始终与BC、AB相交于点M、N，试探索OM与ON的数量关系，并说明理由。
(3)如图3，将(2)中的“正方形”改为“矩形”，其他条件不变，且AB = 4，AD = 6，
FM = x，FN =y，试求y与x之间的关系式。

13、九（1）班合作学习小组为了了解我市餐饮业人员的收入情况，到某餐厅进行调查，他们将了解到的该餐厅所有10名员工月工资情况列表如下：

请你解答他们设计的下列问题（将答案直接填在横线上）：
①该餐厅所有员工的平均工资是元，所有员工工资的中位数是元；
②该餐厅员工工资的众数是元．