
题目列表(包括答案和解析)
 AB,BF=
AB,BF= BC,若?ABCD的面积为S,则四边形BEDF的面积为______.
BC,若?ABCD的面积为S,则四边形BEDF的面积为______. ,请探究线段AE、BF应满足怎样的数量关系,并说明理由.
,请探究线段AE、BF应满足怎样的数量关系,并说明理由.
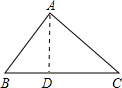 一、阅读理解:
一、阅读理解: (2013•广阳区一模)问题情境:
(2013•广阳区一模)问题情境:| BE |
| CE |
| 2 |
| 2 |
| BE |
| CE |
| ||
| 2 |
| ||
| 2 |
| BE |
| CE |
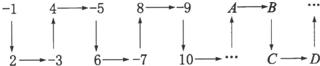
 根据数字排列规律,自主探究,回答下列问题.
根据数字排列规律,自主探究,回答下列问题.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com