某外语学校在圣诞节要举行汇报演出，需要准备一些圣诞帽，为了培养学生的动手能力，学校决定自己制作这些圣诞帽．如果圣诞帽（圆锥形状）的规格是母线长42厘米，底面直径为16厘米．
（1）求圣诞帽的侧面展开图（扇形）的圆心角的度数（精确到度）；
（2）已知A种规格的纸片能做3个圣诞帽，B种规格的纸片能做4个圣诞帽，汇报演出需要26个圣诞帽，写出A种规格的纸片y张与B种规格的纸片x张之间的函数关系式及其x的最大值与最小值；若自己制作时，A、B两种规格的纸片各买多少张时，才不会浪费纸张？
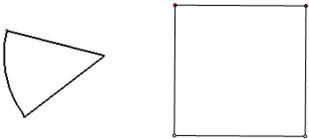
（3）现有一张边长为79厘米的正方形纸片，它最多能制作几个这种规格的圣诞帽（圣诞帽的粘接处忽略不计）．请在比例尺为1：15的正方形纸片上画出圣诞帽的侧面展开图的裁剪草图，并利用所学的数学知识说明其可行性．