练习册

  • 练习册
  • 试题
    对于函数y＝-x2+1的图象.顶点是 .当x 时.函数值y随x的增大而增大,当x 时.函数值y随x的增大而减小,当x 时.函数取得最 值,为 . 【查看更多】

     

    题目列表(包括答案和解析)

    函数y＝－x2的图象开口________，顶点为________，对称轴是________，画出其图象，根据图象指出当x＝－2时，y＝________；当y＝－3时x的值为________．当x为________时，函数有最________值等于________．

    查看答案和解析>>

    关于二次函数y＝x2和y＝2x2以下说法：

    ①它们的图象都是开口向上；

    ②它们的对称轴都是y轴，顶点坐标都是原点(0，0)；

    ③当x＞0时，它们的函数值y都是随着x的增大而增大；

    ④它们的开口的大小是一样的

    其中正确的说法有

    [　　]
    A．

    1个

    B．

    2个

    C．

    3个

    D．

    4个

    查看答案和解析>>

    如图，已知抛物线y＝x2＋bx＋c与x轴交于A、B两点(A点在B点左侧)，与y轴交于点C(0，－3)，对称轴是直线x＝1，直线BC与抛物线的对称轴交于点D．

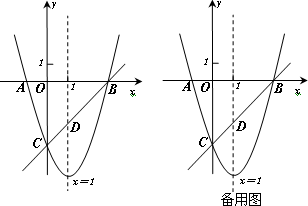
    (1)求抛物线的函数表达式；

    (2)求直线BC的函数表达式；

    (3)点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．

    ①当线段PQ＝AB时，求tan∠CED的值；

    ②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．

    温馨提示：考生可以根据第⑶问的题意，在图中补出图形，以便作答．

    查看答案和解析>>

    在同一直角坐标系中作出函数y＝x2，y＝(x－2)2和y＝(x－2)2＋3的图象，然后根据图象填空：

    抛物线y＝x2的顶点坐标是(　　)，对称轴是________，开口向________；

    抛物线y＝(x－2)2的顶点坐标是(　　)，对称轴是________，开口向________；

    抛物线y＝(x－2)2＋3的顶点坐标是(　　)，对称轴是________，开口向________．

    可以发现，抛物线y＝(x－2)2，y＝(x－2)2＋3与抛物线y＝x2的形状、开口大小相同，只是抛物线的位置发生了变化．把抛物线y＝x2沿x轴向________平移________个单位即可得到抛物线y＝(x－2)2；把抛物线y＝(x－2)2沿y轴向________平移________个单位即可得到抛物线y＝(x－2)2＋3；也就是说，把抛物线y＝x2沿x轴向________平移________个单位，再沿y轴向________平移________个单位即可得到抛物线y＝(x－2)2＋3．

    还可以发现，对于y＝x2，当x＜0时y的值随x值的增大而________，当x＞0时y的值随x值的增大而________；对于y＝k(x－2)2，当x＜2时，y的值随x值的增大而________，当x＞2时，y的值随x值的增大而________；对于y＝(x－2)2＋3，当x＜2时，y的值随x值的增大而________，当x＞2时，y的值随x值的增大而________．

    查看答案和解析>>

    巳知二次函数y＝a(x2－6x＋8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．

    （1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的对称轴上，求实数a的值；
    （2）如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；
    （3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由．

    查看答案和解析>>


    同步练习册答案