
题目列表(包括答案和解析)
已知函数y=-![]() x2,y=-
x2,y=-![]() (x+1)2,y=-
(x+1)2,y=-![]() (x-1)2.
(x-1)2.
(1)在同一直角坐标系中画出它们的图象;
(2)分别说出各个函数图象的开口方向、对称轴和顶点坐标;
(3)分别讨论各个函数的性质.
(4)试说明:分别通过怎样的平移,可以由抛物线y=-![]() x得到抛物线y=-
x得到抛物线y=-![]() (x+1)2和y=-
(x+1)2和y=-![]() (x-1)2.
(x-1)2.
 探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”
探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?” -x),由题意得方程:x(
-x),由题意得方程:x( -x)=3,化简得:2x2-7x+6=0
-x)=3,化简得:2x2-7x+6=0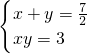 消去y化简后也得到:2x2-7x+6=0,(以下同小明的做法)
消去y化简后也得到:2x2-7x+6=0,(以下同小明的做法)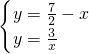 ,此时两个方程都可以看成是函数解析式,从而我们可以利用函数图象解决一些问题.如图,在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下列问题:(完成下列空格)
,此时两个方程都可以看成是函数解析式,从而我们可以利用函数图象解决一些问题.如图,在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下列问题:(完成下列空格) -x),由题意得方程:x(
-x),由题意得方程:x( -x)=3,化简得:2x2-7x+6=0
-x)=3,化简得:2x2-7x+6=0 消去y化简后也得到:2x2-7x+6=0,(以下同小明的做法)
消去y化简后也得到:2x2-7x+6=0,(以下同小明的做法) ,此时两个方程都可以看成是函数解析式,从而我们可以利用函数图象解决一些问题.如图,在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下列问题:(完成下列空格)
,此时两个方程都可以看成是函数解析式,从而我们可以利用函数图象解决一些问题.如图,在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下列问题:(完成下列空格)
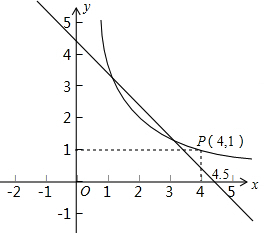 (2012•西城区模拟)探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”
(2012•西城区模拟)探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”| 7 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
|
|
9+
| ||
| 4 |
9+
| ||
| 4 |
9-
| ||
| 4 |
9-
| ||
| 4 |
阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数![]() 的图象为直线
的图象为直线![]() ,一次函数
,一次函数![]() 的图象为直线
的图象为直线![]() ,若
,若![]() ,且
,且![]() ,我们就称直线
,我们就称直线![]() 与直线
与直线![]() 互相平行.
互相平行.
解答下面的问题:
(1)已知一次函数![]() 的图象为直线
的图象为直线![]() ,求过点
,求过点![]() 且与已知直线
且与已知直线![]() 平行的直线
平行的直线![]() 的函数表达式,并在坐标系中画出直线
的函数表达式,并在坐标系中画出直线![]() 和
和![]() 的图象;
的图象;
(2)设直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,过坐标原点O作OC⊥AB,垂足为C,求
,过坐标原点O作OC⊥AB,垂足为C,求![]() 和
和![]() 两平行线之间的距离OC的长。
两平行线之间的距离OC的长。
(3)若Q为OA上一动点,求QP+QB的最小![]() 值,并求取得最小值时Q点的坐标。
值,并求取得最小值时Q点的坐标。
(4)在![]() 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com