
题目列表(包括答案和解析)
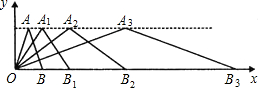
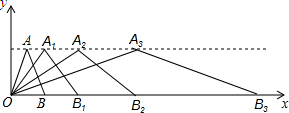
如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
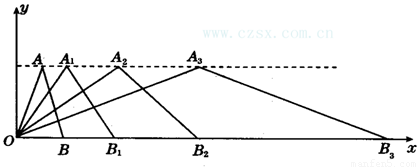
(1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3变换成△OA4B4,则A4的坐标是_______,B4的坐标是_________.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测An的坐标是_______,Bn的坐标是_______.
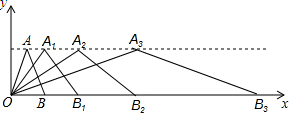
 A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2
A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2 (8,0),B3(16,0)。
(8,0),B3(16,0)。 每次变换前后的三角形有何变化,找出规律,并按规律再将△OA3B3变换成△OA4B4,则A4的坐标为______,B的坐标为_____;
每次变换前后的三角形有何变化,找出规律,并按规律再将△OA3B3变换成△OA4B4,则A4的坐标为______,B的坐标为_____;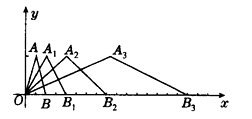
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com