
题目列表(包括答案和解析)
关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ-sinαsinβ②
tan(α+β)=![]() (1-tanα·tanβ≠0)……③
(1-tanα·tanβ≠0)……③
利用这些公式可将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
![]() tan105°=tan(45°+60°)=
tan105°=tan(45°+60°)=![]() =
=![]()
=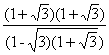 =
=![]() =-(2+
=-(2+![]() )。
)。
根据上面的知识,你可以选择适当的公式解决下面实问题:
|
 A、
A、![]() B、
B、![]()
|
|
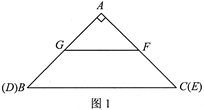
如图1,在Rt△ABC中,∠A=90°,AB=AC,BC=4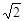 ,另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
,另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
【小题1】填空:GF的长度为________,等腰梯形DEFG的面积为________.
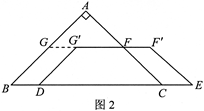
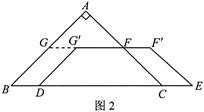
【小题2】操作:固定△ABC,将等腰梯形DEFG以每秒1个单位的速度沿BC方向向右运动,直到点D与点C重合时停止.设运动时间为x秒,运动后的等腰梯形为DEF’G’(如图2)探究:在运动过程中,四边形BDG’G能否为菱形?若能,请求出此时x的值;若不能,请说明理由.
 | |||
 | |||
 ,另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
,另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.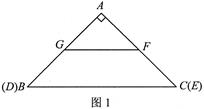 | |||
 | |||
| A、Rt△ABC中AB=3,BC=4,则AC=5 | B、极差仅能反映数据的变化范围 | C、经过点A(2,3)的双曲线一定经过点B(-3,-2) | D、连接菱形各边中点所得的四边形是矩形 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com