
题目列表(包括答案和解析)
 13、张同学是一个NBA迷,周末的一天他在家里做作业,一次他抬头看到墙上镜面里的钟如图所示,那他过
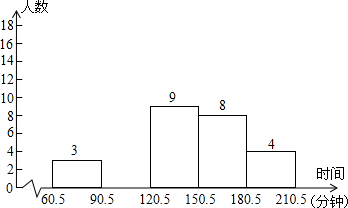
13、张同学是一个NBA迷,周末的一天他在家里做作业,一次他抬头看到墙上镜面里的钟如图所示,那他过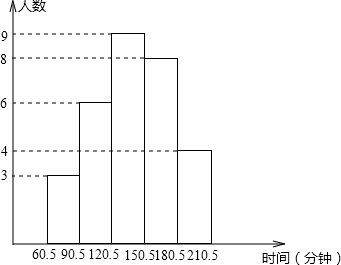 据(时间)进行整理,分成5组,绘制了统计图,请结合图中信息,回答:
据(时间)进行整理,分成5组,绘制了统计图,请结合图中信息,回答: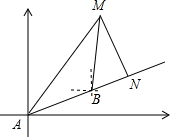 如图,在A黄岩岛东偏北30°方向上有一艘执行巡逻任务的中国海监船,同时在A黄岩岛东偏北60°方向有一艘中国渔船M正在海上作业.当我海监船向前行进到1800米的B处时,接到渔船发来的求救信号,信号显示,我渔船被菲律宾军舰“德尔毕拉尔”号扣留,即将沿MN方向将我渔船带回菲律宾.此时测得“德尔毕拉尔”号在我海监船的北偏东15°处,若MN⊥AB,我海监船继续向前行驶多少米可在N处拦截到“德尔毕拉尔”号?
如图,在A黄岩岛东偏北30°方向上有一艘执行巡逻任务的中国海监船,同时在A黄岩岛东偏北60°方向有一艘中国渔船M正在海上作业.当我海监船向前行进到1800米的B处时,接到渔船发来的求救信号,信号显示,我渔船被菲律宾军舰“德尔毕拉尔”号扣留,即将沿MN方向将我渔船带回菲律宾.此时测得“德尔毕拉尔”号在我海监船的北偏东15°处,若MN⊥AB,我海监船继续向前行驶多少米可在N处拦截到“德尔毕拉尔”号?| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com