
题目列表(包括答案和解析)

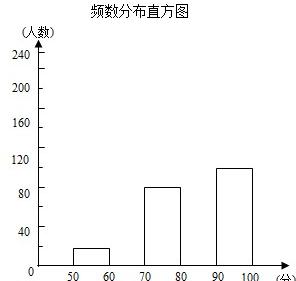
| 分组(分) | 频数 | 频率 |
| 90~100 | 100 | 0.25 |
| 80~90 | ||
| 70~80 | 80 | 0.20 |
| 60~70 | 0.10 | |
| 50~60 | 20 | 0.05 |
| 合计 | 400 | 1.00 |
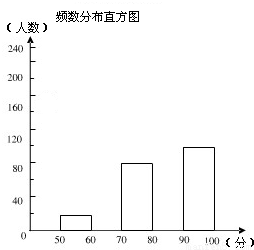
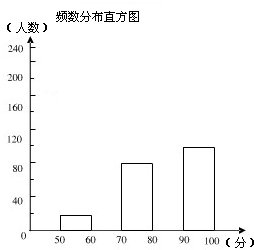 图.
图.| 分组(分) | 频数 | 频率 |
| 90~100 | 100 | 0.25 |
| 80~90 | ||
| 70~80 | 80 | 0.20 |
| 60~70 | 0.10 | |
| 50~60 | 20 | 0.05 |
| 合计 | 400 | 1.00 |
 (2012•黄石)某校从参加计算机测试的学生中抽取了60名学生的成绩(40~100分)进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图(其中70~80段因故看不清),若60分以上(含60分)为及格,试根据图中信息来估计这次测试的及格率约为
(2012•黄石)某校从参加计算机测试的学生中抽取了60名学生的成绩(40~100分)进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图(其中70~80段因故看不清),若60分以上(含60分)为及格,试根据图中信息来估计这次测试的及格率约为

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com