（2013•白下区一模）实际情境
王老师骑摩托车想尽快将甲、乙两位学生从学校送到同一个车站．由于摩托车后座只能坐1人，为了节约时间，王老师骑摩托车先带着乙出发，同时，甲步行出发．
已知甲、乙的步行速度都是5km/h，摩托车的速度是45km/h．
方案预设
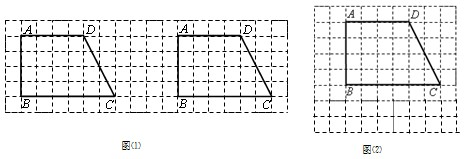
（1）预设方案1：王老师将乙送到车站后，回去接甲，再将甲送到车站．图①中折线A-B-C-D、线段AC分别表示王老师、甲在上述过程中，离车站的路程y（km）与王老师所用时间x（h）之间的函数关系．
①学校与车站的距离为km；
②求出点C的坐标，并说明它的实际意义；
（2）预设方案2：王老师骑摩托车行驶ah后，将乙放下，让乙步行去车站，与此同时，王老师回去接甲并将甲送到车站，王老师骑摩托车一共行驶

5

6

h．图②中折线A-B-C-D、线段AC、线段BE分别表示王老师、甲、乙在上述过程中，离车站的路程y（km）与王老师所用时间x（h）之间的函数关系．求a的值．
优化方案
（3）请设计一种方案，使甲、乙两位学生在出发50min内（不含50min）全部到达车站．
（要求：1．不需用文字写出方案，在图③中画出图象即可；2．写出你所画的图象中y与x的含义；3．不需算出甲、乙两位学生到达车站的具体时间！）

25、将一直角梯形放在如图所示的正方形网格（图中每个小正方形的边长均为一个单位长）中，请你按照以下要求进行合理设计﹙说明：直接画出图形，不要求写分析过程．﹚
（1）在图1中画一条直线将一个直角梯形分成面积相等的两部分，分别设计出两种不同的分割方法；
（2）在图2中将直角梯形进行适当分割后拼接成一个与所给直角梯形面积相等的正方形，用虚线画出分割线，再用实线画出拼接而成的正方形．

15、联系实际背景，说明代数式6a²的实际意义．

某单位计划10月份组织员工到A地旅游，人数估计在10-25人之间．甲、乙两家旅行社的服务质量相同，且报价均为200元．该单位上门联系时，甲社表示可给予每位游客七五折优惠；乙社表示可先免去一位游客的旅游费用，其余游客八折优惠．设该单位去A地的旅游人数为x，若选择甲社，则所需总费用为y₁元；若选择乙社，则所需总费用为y₂元．
（1）分别求出y₁、y₂与x的函数关系式；
（2）在同一平面直角坐标系中，画出上述两个函数的图象；
（3）求出两条直线的交点坐标，并说明它的实际意义．

15、联系实际背景，说明代数式6a²的实际意义．