
题目列表(包括答案和解析)
| 3 |
| x |
| 3 |
| x |
阅读材料,并解答问题。
我们已经学过了一元一次不等式的解法,对于一些特殊的不等式,我们用作函数图象的方法求出它的解集,这也是《数学新课程标准》中所要求掌物的内容。例如:如何求不等式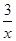 ﹥x+2的解集呢? 我们可以设
﹥x+2的解集呢? 我们可以设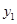 =
=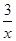 ,
,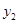 =x+2.然后求出它们的交点的坐标,
并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x
=x+2.然后求出它们的交点的坐标,
并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x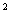 -x>x+3的解集.
-x>x+3的解集.
(1)设函数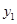 = ,
= , 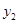 =
=
(2)两个函数图象的交点坐标为
(3)在所给的直角坐标系中画出两个函数的图象(不要列表).
(4)观察发现:不等式x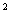 -x>x+3的解集为
-x>x+3的解集为

阅读材料,并解答问题。
我们已经学过了一元一次不等式的解法,对于一些特殊的不等式,我们用作函数图象的方法求出它的解集,这也是《数学新课程标准》中所要求掌物的内容。例如:如何求不等式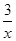 ﹥x+2的解集呢? 我们可以设
﹥x+2的解集呢? 我们可以设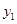 =
=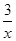 ,
,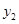 =x+2.然后求出它们的交点的坐标, 并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x
=x+2.然后求出它们的交点的坐标, 并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x -x>x+3的解集.
-x>x+3的解集.
(1)设函数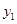 = ,
= , 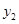 =
=
(2)两个函数图象的交点坐标为
(3)在所给的直角坐标系中画出两个函数的图象(不要列表).
(4)观察发现:不等式x -x>x+3的解集为
-x>x+3的解集为 
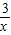 >x+2的解集呢我们可以设y1=
>x+2的解集呢我们可以设y1=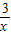 ,y2=x+2.然后求出它们的交点的坐标,并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“x<-3或0<x<1”
,y2=x+2.然后求出它们的交点的坐标,并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“x<-3或0<x<1”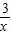 >x+2的解集呢我们可以设y1=
>x+2的解集呢我们可以设y1=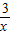 ,y2=x+2.然后求出它们的交点的坐标,并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“x<-3或0<x<1”
,y2=x+2.然后求出它们的交点的坐标,并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“x<-3或0<x<1”湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com